Do AI Reasoning Models Abstract and Reason Like Humans?

Going beyond simple accuracy for evaluating abstraction abilities

Here I’ll summarize a new paper from my group:

Do AI Reasoning Models Perform Humanlike Abstract Reasoning?

The Abstraction and Reasoning Corpus (now called ARC-AGI-1) has become popular as a test of abstract reasoning ability in AI models. ARC is meant to be a test of abstraction and analogy, based on “core knowledge” priors, especially objectness, along with basic spatial and geometric concepts such as “inside vs. outside”, “top vs. bottom”, basic semantic concepts such as “same vs. different”, and basic numerical / size concepts such as “largest vs. smallest”.

For example, here’s a task from the ARC-AGI-1 public evaluation corpus. The task gives three demonstrations of a transformation rule that maps an input grid to an output grid. The task is to apply the analogous transformation to the test input grid to generate a test output grid.

For this task, the rule is something like “Extract the sub-grid inside the largest hollow rectangle.” Intended abstractions here include “largest”, “hollow”, “rectangle”, “inside”, and “extract sub-grid”.

AI reasoning models like OpenAI’s o3 have exceeded average human accuracy on ARC-AGI-1. However, just looking at their accuracy does not tell the whole story. Are they getting the right answers for the “right” reasons—i.e., are they grasping the abstractions intended by the humans that created the tasks? Or, alternatively, are they solving tasks using less abstract, less generalizable, unintended patterns (“shortcuts”)? Large neural networks are often known to discover such unintended shortcuts to perform well on benchmarks, but then are not able to generalize well outside their training “distribution”.

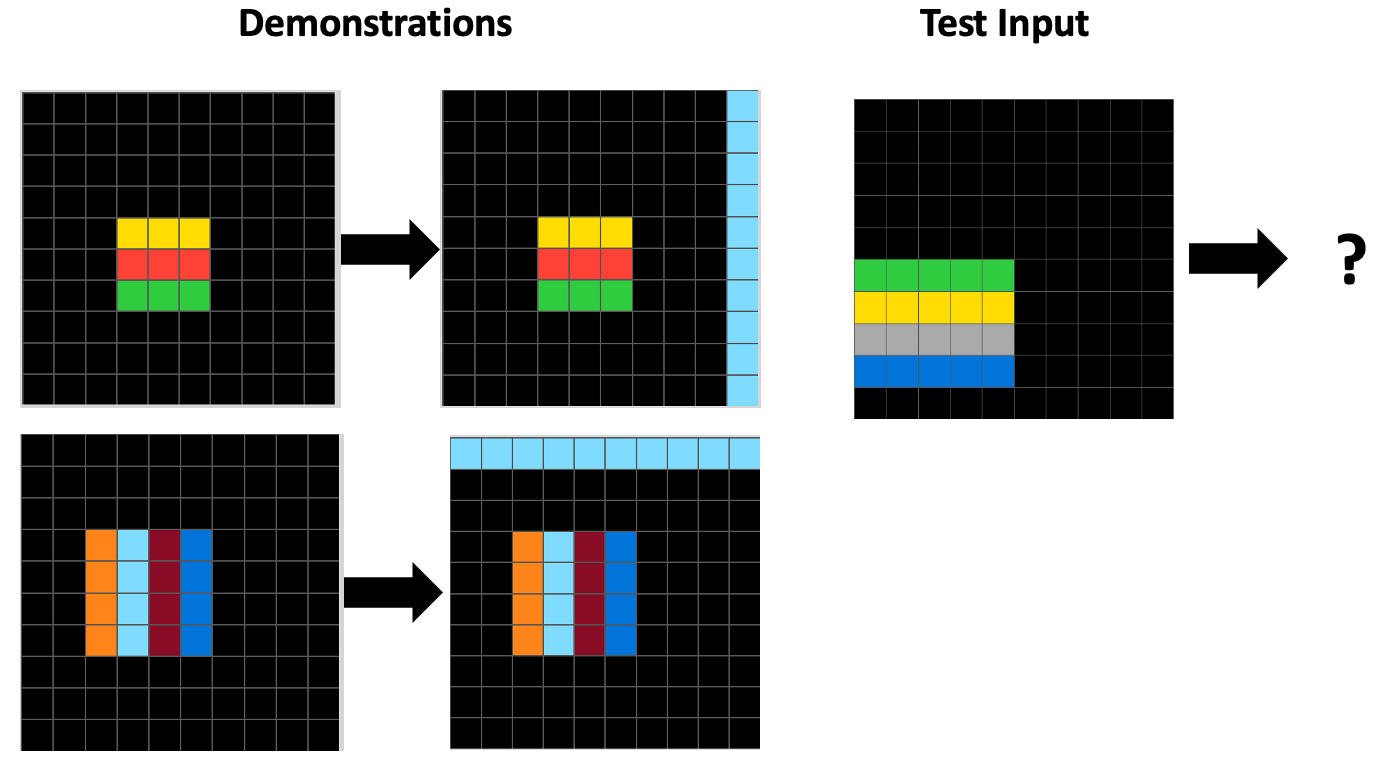
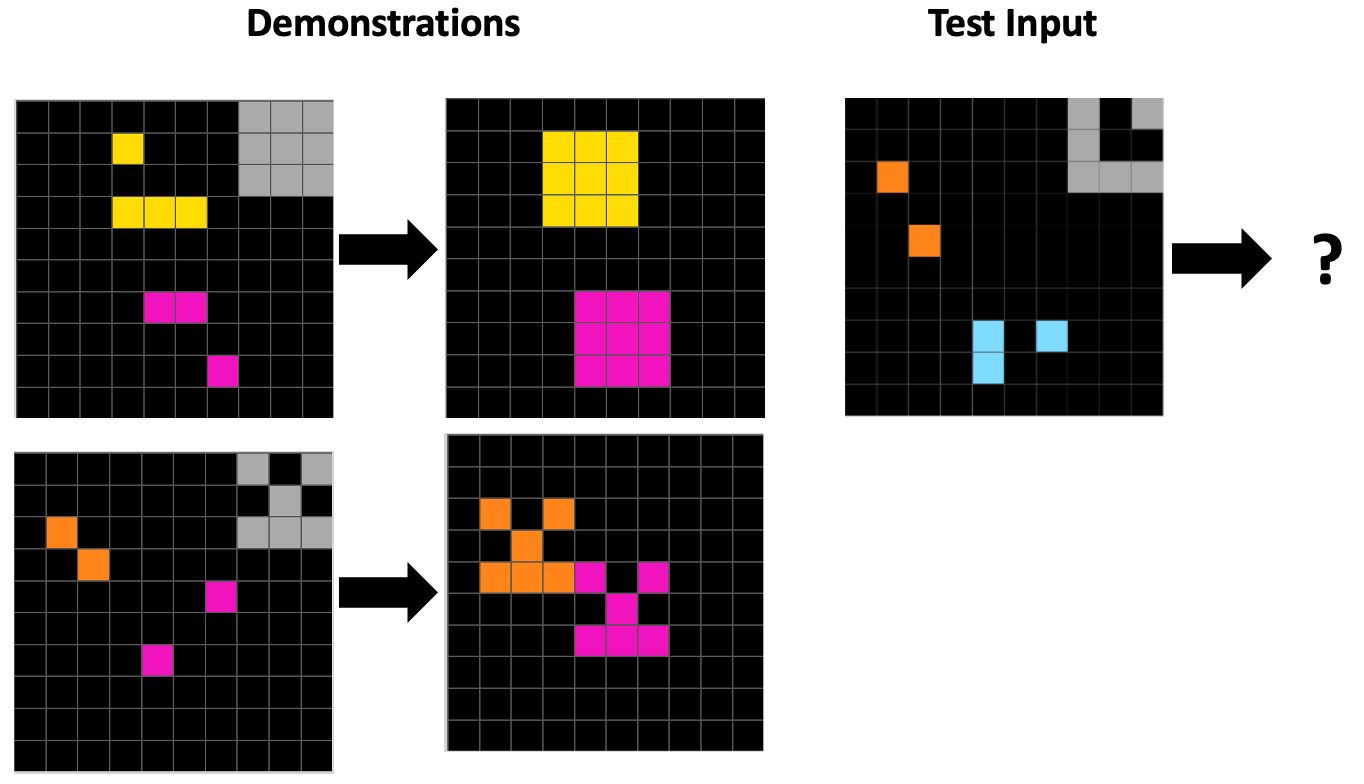
For our paper, we investigated this question by evaluating several reasoning models, including OpenAI’s o3, Anthropic’s Claude Sonnet 4, and Google’s Gemini 2.5 Pro, on 480 tasks from ConceptARC, a benchmark in the ARC domain whose tasks isolate various core concepts. Here are two ConceptARC tasks: the first one is an example of the “horizontal vs. vertical” concept; the second one is an example of the “complete the shape” concept.

For the reasoning models, we experimented with both textual inputs (like those used in the ARC Prize competition, in which each grid is input as an integer matrix, with integers 0–9 representing colors) and visual inputs (like those given to humans).

We prompted the models not only to generate an output grid, but also to state the natural-language transformation rule that describes the demonstrations and can be applied to the grid. We manually rated every generated rule as correct as intended (the rule captures the intended abstractions), correct but unintended (the rule correctly describes the demonstrations but doesn’t capture the intended abstractions), and incorrect (the rule does not work for demonstrations). We compared these with rules generated by humans.

For example, below are examples of rules generated by humans and by Gemini 2.5, o3, and Claude Sonnet 4 (all using textual inputs and medium reasoning effort) on the “horizontal vs. vertical” task shown above. Note that humans in our study saw images representing the grids, like the ones you see above, but models were given arrays of numbers to represent each grid. In the rules generated by AI models below, “8” is the integer representing the light blue color.

Human: If the lines are horizontal, draw a full vertical light blue line on the far right. If the lines are vertical, draw a full horizontal light blue line at the very top. [We rated this “correct as intended.]

Gemini: Find the contiguous block of non-zero numbers. If the numbers in the block are constant in each row, fill the rightmost column of the grid with 8. If the numbers are constant in each column, fill the topmost row of the grid with 8. [We rated this “correct as intended”, even though it was not the way a human would describe horizontal vs. vertical lines.]

o3: Determine whether the coloured stripes in the picture run horizontally or vertically. If they are horizontal, paint the entire empty edge column that is farthest from the stripes with colour 8; if they are vertical, paint the entire empty edge row that is farthest from the stripes with colour 8 (on a tie pick the uppermost/leftmost edge). Leave every other cell unchanged. [This was close to a correct rule, but it focuses on “farthest from the stripes”, which was not intended, so this was rated “correct but unintended”.]¹

Claude: If input contains value 8, fill first row with 8s; if input does not contain 8, fill last column with 8s. [Here, Claude focuses on a shallow feature—are there any light-blue (“8”) cells? The model’s rule does not mention objects or notions of horizontal vs. vertical lines. By coincidence, the rule is correct on the demonstrations and the given test, but it is right for the wrong reason—“correct but unintended”.]

Here is a similar analysis of rules for the “complete the shape” task given above. Note that “5” represents the gray color.

Human: The object in the upper right is the “sample” object. Do not include this object in your drawing. Using the same colors as the two objects to the left, make them look exactly like the sample object by filling them in. [This rule was “correct as intended”.]

Gemini: For each color C other than 5, find the bounding box of all cells of that color and fill the entire box with C. All cells with color 5 are replaced by 0. If the bounding boxes of different colors overlap, the cell takes the value of the highest color. [This rule doesn’t work for the second demonstration, so was rated as “incorrect”.]

o3: Erase the colour that occurs most often. For every other colour locate the pixel with the smallest row and column indices; from that cell draw a fixed 3×3 square (rows r..r+2, columns c..c+2). If the colour originally has three or more pixels, fill the whole square with that colour; if it has exactly two pixels, fill the square with the 6-cell arrow pattern (1 0 1 / 0 1 0 / 1 1 1). [Here o3 is giving detailed instructions for the two demonstrations, but not in a way that will generalize beyond these descriptions. A great example of a “correct but unintended” rule.]

Claude: Remove all 5s. For each remaining color: if exactly 2 cells exist, apply a 3x3 T-shaped template (pattern: X.X/.X./XXX) starting from the top-left corner of the bounding box. If 3 or more cells exist, fill the entire bounding rectangle with that color. [Similar to o3’s rule, this one describes the two demonstrations in exact detail, but doesn’t capture the intended abstraction of completing a shape according to an example shape.]

We found that while o3, Claude, and Gemini approach or exceed human accuracy on these tasks with textual inputs, they are substantially more prone to use unintended “shortcuts” to solve the tasks than do humans. Interestingly, unlike humans, these models tended to describe grids in terms of pixels, colors, columns, and rows rather than in terms of objects, so, at least in the textual setting, they do not seem to have a strong humanlike “objectness” prior.

With visual inputs, these models all do quite poorly on generating accurate grids. However, they do generate “correct as intended” rules more often than they generate correct grids, showing that in some cases they are able to process visual input correctly.

The main take-home message of our paper is that evaluations like those done for the ARC Prize, using accuracy alone, may be overestimating abstract reasoning ability of these models in the textual setting. On the other hand, using accuracy alone may be underestimating the ability for abstract reasoning in the visual setting. It is essential to go beyond accuracy in such evaluations!

One might ask, why should we care if AI models solve these tasks using humanlike abstractions or if they use “shortcuts”? To answer: the ability to grasp and reason with humanlike abstractions is what the ConceptARC benchmark—and I believe, the ARC benchmark as well—was designed to test. Using such abstractions is how we humans are able to understand our world, predict probable outcomes of our decisions, and to efficiently deal with novelty. These are all things we want AI systems to do in more trustworthy ways.

Moreover, if we humans are to work together with AI systems, it’s essential to develop AI models that are better at grasping our abstractions so that they will be able to understand our intentions and explain their reasoning in ways understandable to us.

Want more details? Read the paper here.

1. It is interesting to note that the textual prompt given to these models did not mention that the integers represented colors, but o3 knew that anyway, and mentioned in some cases that these were “ARC” tasks. Also I was struck by the weird (though irrelevant) fact that in the rules it generated, o3 spelled “color” in the British way, but spelled it in the American way in its reasoning traces.