An “AI Breakthrough” on Systematic Generalization in Language?

A Fun Puzzle

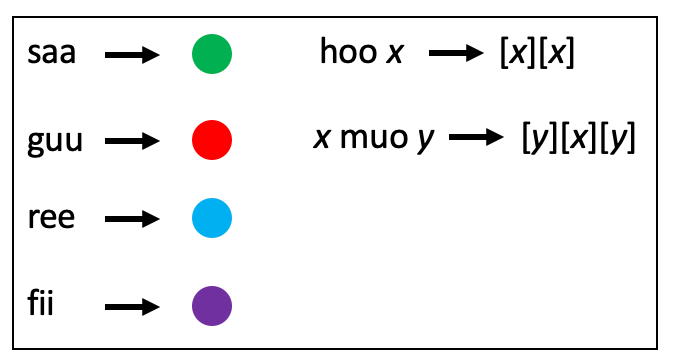
Here’s a fun puzzle for you.  I’ll give you six words in an alien language: saa, guu, ree, fii, hoo, and muo.  Figure 1 gives a diagram showing how either single words or combinations of words result in combinations of colored circles.  Given the example sentences, what combination of colored circles should result from the query sentence hoo guu muo hoo fii?  (Read further for the answer.)

Figure 1: A fun puzzle.

Systematic Generalization in Language

This small puzzle—I’ll call it Puzzle 1—illustrates the crucial notions of compositionality, systematicity, and productivity in language understanding.

• Compositionality: The meaning of a phrase or sentence is a function of the meaning of its component words and the way in which those words are combined.  For example, in the puzzle’s phrase hoo saa, the meaning of saa is “green circle” and the meaning of hoo is “double,” so the meaning of hoo saa is “double green circle.”

• Systematicity: If you can understand or produce a particular sentence, you can also understand or produce certain related sentences.  For example, anyone who understands “the dog was asleep but the cat was awake” should also be able to understand “the dog was awake but the cat was asleep.”  Anyone who understands “the blue vase was on top of the green table” can also understand “the blue table was on top of the green vase.”  Systematicity is an ability that is enabled by a compositional understanding of language, and humans are very adept systematic language users.  Puzzle 1 illustrates systematicity: if you understand hoo ree muo saa you should also understand hoo saa muo ree.

• Productivity: Language users have the potential ability to generate—and understand—an infinite number of sentences.  For example, if you can generate “A blue vase is on top of a green table,” you should also be able to generate “A blue vase is on top of a green table, which is on top of a blue table, which is on top of a green vase,” and so on.  Or if you learn a new word like “workaholic,” you can easily extend it to “shopaholic,” “chocaholic,” “talkaholic,” etc.  Like systematicity, productivity is enabled by our compositional language abilities.

Taken together, these linguistic abilities have been called “systematic generalization.”  Humans are very good at systematic generalization—it’s what enables you to give the answer to Puzzle 1, shown in Figure 2:¹

Figure 2: Answer to the fun puzzle.

In the late 1980s, the philosophers Jerry Fodor and Zenon Pylyshyn wrote an influential paper claiming that while “symbolic,” rule-based AI systems could easily capture systematic generalization in language, such abilities were not achievable with connectionist (i.e., neural network) architectures.

Indeed, it has been shown in many research efforts over the years that neural networks struggle with systematic generalization in language. While today’s most capable large language models (e.g., GPT-4) give the appearance of systematic generalization—e.g., they generate flawless English syntax and can interpret novel English sentences extremely well—they often fail on human-like generalization when given tasks that fall too far outside their training data, such as the made-up language in Puzzle 1. 

A recent paper by Brenden Lake and Marco Baroni offers a counterexample to Fodor & Pylyshyn’s claims, in the form of a neural network that achieves “human-like systematic generalization.” In short, Lake & Baroni created a set of puzzles similar to Puzzle 1 and gave them to people to solve.  They also trained a neural network to solve these puzzles using a method called “meta-learning” (more on this below).  They found that not only did the neural network gain a strong ability to solve such puzzles, its performance was very similar to that of people, including the kinds of errors it made.

The Lake & Baroni paper was covered broadly in the media. For example, Nature called it an “AI Breakthrough” and Scientific American described it as a method for helping AI “generalize like people do.”  Our local AI reading group delved into this paper; I found the discussion really interesting and thought it would be useful to cover it here. In this post I’ll discuss what the paper does and to what extent it fulfills (or does not fulfill) these enthusiastic characterizations.

Tasks, Grammars, and Meta-Grammars

For their study, Lake & Baroni created a large number of “tasks”—puzzles similar to Puzzle 1.  Each task was created automatically from an underlying “grammar”, a set of rules for translating sequences of symbols to color configurations.  For example, a grammar for Puzzle 1 is shown in Figure 3:

Figure 3: A grammar for Puzzle 1.

Here, “[ ]” around a symbol means “replace by the corresponding color pattern”, and the variables x and y can each be either be a primitive color word or a function (like hoo saa) or any composition of functions (like hoo saa muo ree).  Here the order of functions in the grammar indicates the order in which they must be applied (e.g., hoo is applied before muo). 

You can verify that all the example sentences from Puzzle 1 can be generated from this grammar.  Lake & Baroni used such grammars to generate new tasks by listing a set of primitive color words and their corresponding colors, and then generating a small number of example and query sentences from the various function rules in the grammar, using random choices for filling in variables x and y.

Given a large number of example sentences generated by a very simple grammar like this, it isn’t hard to figure out the underlying rules of the grammar.  But Lake & Baroni wanted to teach neural networks to solve a more general task: performing systematic generalization from just a few examples on tasks generated from different grammars.

To automatically generate tasks from different grammars, Lake & Baroni needed an automatic way to generate different grammars—namely, a “meta-grammar.”  The meta-grammar had simple rules for generating grammars like the one in Figure 3: any grammar would contain mappings from words to colored circles, as well as a small set of functions, each of which takes one or two arguments and maps to a new simple configuration of the arguments (with a limitation on the length of each rule).  For example, Figure 4 shows a new grammar I generated from the meta-grammar. 

Figure 4: Another possible grammar.

Human Studies

In order to benchmark humans’ systematic generalization abilities on these tasks, Lake & Baroni recruited 30 participants on Amazon Mechanical Turk, and tested them on a variety of such puzzles, each generated from a different grammar.  Before being tested, the participants were taught how to solve the puzzles starting with queries involving single functions and then moving to more complex function compositions.  The participants who did not succeed during the learning phase did not participate in the test phase; in the end, 25 participants were tested.  As reported in Nature, “[P]eople excelled at this task; they chose the correct combination of coloured circles about 80% of the time, on average. When they did make errors, the researchers noticed that these followed a pattern that reflected known human biases.”

Training a Neural Network for Systematic Generalization

To teach neural networks to solve these tasks, Lake & Baroni used a transformer architecture—a specific kind of deep neural network—with about 1.4 million parameters (small compared to behemoths like GPT-4).  As illustrated below in Figure 5, the input to the transformer is a puzzle like Puzzle 1, with the query sentence (the one to be solved) concatenated with the example sentences.² The network is trained to output the answer to the puzzle: a sequence of colored circles corresponding to the query sentence.

Figure 5: Illustration of the transformer’s input and output.

The key contribution of Lake & Baroni’s paper is the training method for the network, a form of “meta-learning.”  Note that an individual puzzle is itself a learning task: the puzzle solver learns from a small set of examples (the example sentences) to infer the meaning (colored circle sequence) of a new sentence (the query sentence).  By giving many examples of such learning tasks to the network—ones generated from different grammars—the network can be said to be “meta-learning,” that is, learning more generally how to perform the small learning tasks.

Lake & Baroni call their network training method “Meta-Learning for Compositionality” (MLC).  The goal is to train the network not for a specific task, but rather to achieve the kind of general systematic compositional generalization seen in humans. The MLC network is trained over a series of “episodes.”  For each episode, a new grammar (like the ones in Figures 3 and 4) is generated from the meta-grammar.  The new grammar then is used to generate a set of example sentences and a set of query sentences.  Each query sentence, paired with all the example sentences, is given to the Transformer network, as illustrated in Figure 5.  For each query the network predicts a sequence of tokens, and the weights are updated to make the correct sequence more likely.  This process continues for 100,000 episodes. 

There’s a twist, though.  I mentioned above that humans tested on these tasks get the right answer about 80% of the time.  Since Lake & Baroni wanted their neural network to be human-like in its generalization behavior, the network was trained with the correct answer on only 80% of the Query Sentences.  On the other 20%, the “correct answer” was actually an incorrect answer that reflected the kinds of errors humans were seen to make.

After training, the MLC network was tested on a set of new puzzles, produced by new grammars generated by the same meta-grammar used in training.  On these new puzzles, the network’s performance was very similar to that of humans: it got the actual (“systematic”) correct answer about 82% of the time (humans got 81% correct), and the errors it made were similar to those made by humans.  This similarity in performance is the meaning of the term “human-like” in the paper’s title (“Human-like systematic generalization through a meta-learning neural network”). 

Interestingly, when Lake & Baroni gave the same new puzzles to GPT-4, that system gave a correct answer only 58% of the time.  Of course, GPT-4 was not trained on these kinds of puzzles, beyond the examples given in the prompt, so in some sense 58% is impressive, but it is far below the performance of humans, who were also only minimally trained on such puzzles.

Lake & Baroni experimented with variations on the MLC algorithm and with giving the same tasks to other neural networks; they also tested MLC on other types of systematic generalization problems.  I won’t cover all this here; if you’re interested in the details, take a look at the paper.

My Thoughts and Questions

I found this paper to be a fascinating proof-of-principle—that is, it shows that Fodor & Pylyshin’s claims about neural networks do not hold for a particular class of tasks testing systematic generalization.  As the authors point out, they were able to achieve systematic generalization without any “symbolic machinery,” which Fodor & Pylyshyn claimed would be necessary.

But to what extent does the MLC method actually achieve “human-like systematic generalization”?  In this paper, “human-like” means having performance (both successes and failures) similar to that of humans on a specific class of generalization task.  But even on this particular task, the MLC system is quite unhuman-like, in that it requires being trained on hundreds of thousands of examples of these tasks, whereas humans need only minimal training to achieve the same performance, because they can build on very general skills and training that has occurred over their lifetimes.  Moreover, humans easily adapt these skills to learn to solve different classes of generalization tasks (e.g., the same kind of tasks given to MLC but with words they hadn’t seen before, or with longer sentences, or generated via a different “meta-grammar”).  MLC, in contrast, would not be able to solve such tasks—one might say that the system is not able to “meta-generalize.”  As Scientific American reported:

[T]he training protocol helped the model excel in one type of task: learning the patterns in a fake language. But given a whole new task, it couldn’t apply the same skill. This was evident in benchmark tests, where the model failed to manage longer sequences and couldn’t grasp previously unintroduced ‘words.’

Importantly, notions of “meta-learning” and “meta-generalization” are, for humans, simply part and parcel of ordinary learning and generalization.  The MLC system is an advance for AI, but remains unhuman-like in its failure to more broadly generalize its compositional skills like people can.  It’s still an open question whether “symbolic components” a la Fodor & Pylyshyn will be needed for such broader generalization abilities, which are are the core of the “general” intelligence humans possess.

One thing that confused me in this paper was the explicit training to make the system act more “human-like.”  As I described above, after cataloging the frequency and kinds of errors made by humans on these tasks, Lake & Baroni trained their network explicitly on examples having the same frequency and kinds of errors.  They then observed that, on new tasks, the trained model produced error frequencies and types similar to those of humans.  But given the explicit training, I didn’t understand why this would surprising, and I didn’t see what insights such results provide.  It would have been more interesting, I think, if they had trained their system in a more general way, and the “human-like” performance had emerged.  As is, I wasn’t sure what this result was meant to show.

In conclusion, this is a very interesting proof-of-principle paper on systematic generalization in neural networks.  I wouldn’t characterize it as an “AI breakthrough”—to me, that would imply a system with more broad and robust generalization abilities—but definitely as a promising method on an important topic, one that deserves further research and scrutiny.

Thanks to Alessandro Palmarini, Martha Lewis, and Una-May O’Reilly for helping me think about this paper!

Postscript

On a different topic, there are a few recent articles and talks from me that readers of this Substack might find interesting:

I am writing occasional non-technical columns focused on AI for Science Magazine.  My columns so far:

·      AI's Challenge of Understanding the World

·      How Do We Know How Smart AI Systems Are?

I’m working on a new one about the meaning of “AGI.”  Stay tuned!

In November 2023 I gave a Santa Fe Institute Public Lecture called “The Future of AI”— you can watch it here.

My SFI collaborators and I compared humans, GPT-4 and GPT-4-Vision on our ConceptARC abstract reasoning benchmark.  Here’s the paper.

I participated in a survey of selected AI researchers on “the state and future of deep learning.”  Here’s the paper.

Till next time!

1. If you didn’t get this answer, it’s probably because of confusion over ordering.  You can think of the words hoo and muo as functions that operate on color words. hoo takes the word following it and doubles the corresponding color. muo takes the word following it, doubles the corresponding color, and puts the color corresponding to the preceding word in the middle of the pair.  Moreover, hoo and muo can be combined; the example combinations show that hoo should be applied first, and then muo should be applied to the result.

2. As is standard for transformers, each of the “tokens” (words, colored circles, arrows, and sentence separator symbols) is input to the network in the form of an “embedding vector”—a list of numbers representing that token.